Aller au contenu principal

Camera3D

Cette classe représente une caméra dans un espace 3D, et sert à effectuer des calculs de projection de points 3D sur l'écran de la caméra, et inversement de l'écran de la caméra vers l'espace. On a donc besoin pour cette classe de connaître les paramètres intrinsèques de la caméra, ainsi que la résolution des images captées.

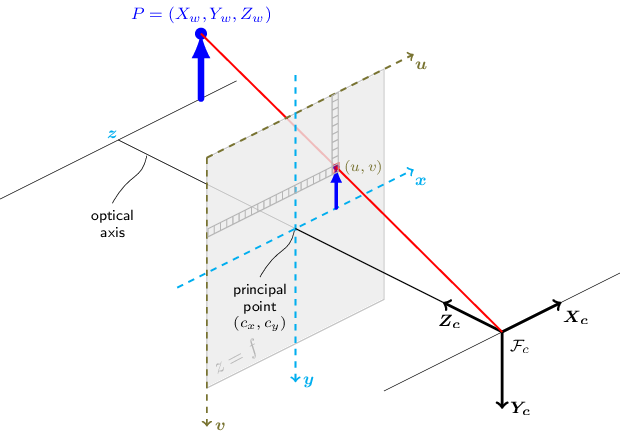
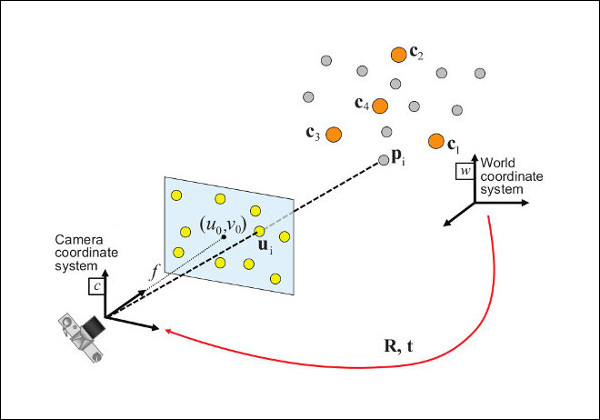
A partir des paramètres intrinsèques (propriétés de la caméra) et extrinsèques (position et rotation de la caméra), on peut effectuer des projections de points en suivant le modèle du sténopé (voir ici pour le détail des calculs)

Cette classe possède 3 méthodes principales :

  • screen_to_space_coords : permet de projeter un pixel dans l'espace. Pour cela, si la distance est fournie on va calculer les coordonnées du point correspondant à ce pixel et à cette distance de l'écran, ou si la distance n'est pas fournie, on calcule la position du point correspondant à ce pixel en projetant le point au sol (d'équation y = 0)
  • space_to_screen_coords : permet de projeter un point de l'espace sur l'écran de la caméra
  • project_depth : permet de projeter une image de profondeur en un ensemble de points 3D, en utilisant la même méthode que pour screen_to_space_coords. Cependant, la rotation et la translation de la caméra ne sont pas appliquées

pinhole_model

Projection directe (de l'espace vers l'écran)​

Pour la méthode space_to_screen_coords, on se base directement sur le modèle du sténopé pour projeter le point. Il s'agit simplement d'un calcul matriciel. On a besoin pour ça de la matrice de projection, que l'on obtient en multipliant les matrices de paramètres intrinsèques et extrinsèques (fait à l'initialisation de l'objet). Puis l'on multiplie la matrice de projection avec le vecteur position du point, et l'on obtient les coordonnées sur l'écran du point, que l'on normalise ensuite.

projection_equation

Ici, le vecteur position est composé des 3 coordonnées X, Y, Z du point, et les coordonnées sur l'écran sont u et v (multipliées par un scalaire s). Les coordonnées physiques du point sont en mètres, et les coordonnées sur l'écran sont en pixels.

Projection inverse (de l'écran vers l'espace)​

La projection inverse est moins évidente, car la matrice de projection calculée précédemment n'est pas inversible (matrice de dimension 3x4).
La solution que j'ai utilisée ici est :

  • Multiplier les coordonnées du pixel avec la matrice des paramètres intrinsèques inverse; on obtient les coordonnées du point dans le repère de la caméra, à 1 mètre de celle-ci
  • Appliquer la rotation de la caméra aux coordonnées du point; on obtient dans l'espace le vecteur différence entre la position du point et celle de la caméra
  • Multiplier ce vecteur par la distance du point à la caméra, et additionner le vecteur obtenu avec la position de la caméra. On obtient alors les coordonnées du point dans l'espace

inverse_projection

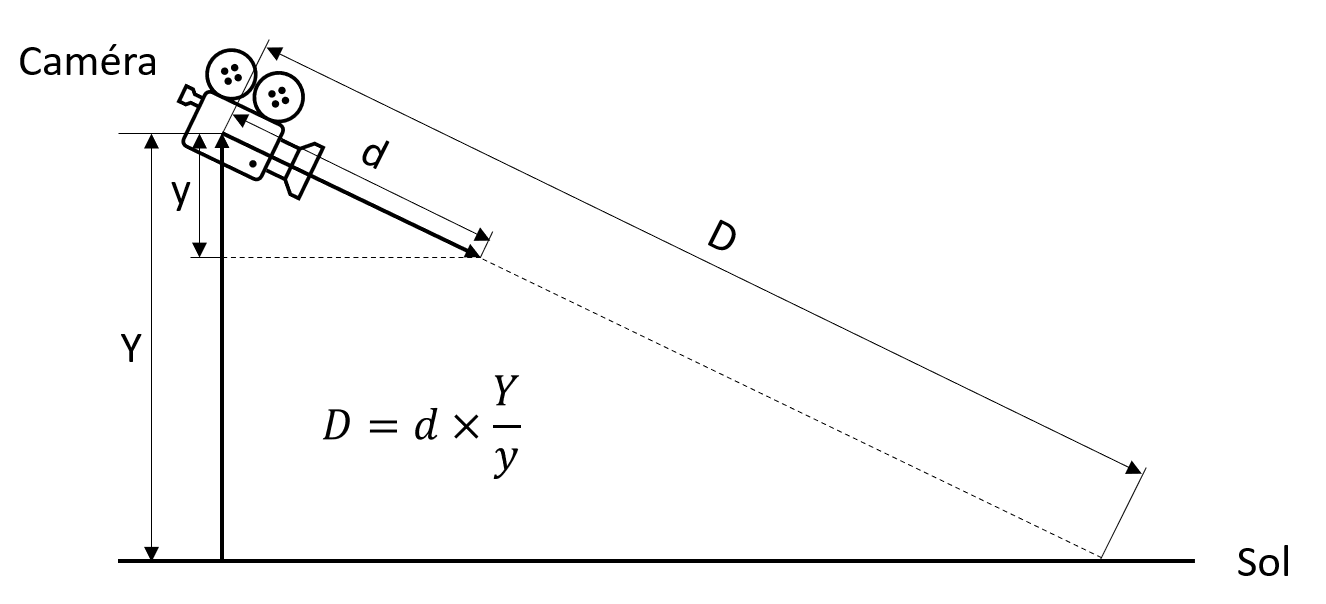
Si la distance du point à la caméra n'est pas spécifiée, on veut que le point soit projeté sur le sol. Pour cela, on calcule la distance en appliquant le théorème de Thales au vecteur dans l'espace entre la position du point et celle de la caméra avec le vecteur vertical vers le haut.

inverse_projection_distance

Pour la projection de la profondeur de l'image, pour aller plus vite les coordonnées des pixels sont pré-calculées à l'initialisation. On multiplie alors par la matrice de paramètres intrinsèques inverse, puis on multiplie par la distance pour obtenir les points en 3D.